
I do not know who, when, or where this iconic mathematical representation was developed. It is, however, one of the most powerful and ubiquitous of all mathematical images, and I think the most important. It is taught to 2nd graders and used by STEAM professionals. It is called a function machine, and it represents the way we think about change, cause and effect, and technology as well as mathematical functions. For since the dawn of the industrial age we have pictured our world as a machine, as a “rule” that converts (connects) an input into an output.
 This image of James Watt’s early steam engine shows a variety of inputs, outputs, and connections between them. On the left side, the steam from heating water provides the input to the rule, the big piston outputs the steam into the vertical motion of the piston. That vertical motion, through the rod connecting the piston to the lever, is now a new input. The lever is a rule changing the direction of the motion connecting it to a wheel on the right side. This rule converts vertical motion to circular motion. The lights lines are belts to link the circular motion, yes a link is a rule to drive some other outputs, one of which is the governor. The governor
This image of James Watt’s early steam engine shows a variety of inputs, outputs, and connections between them. On the left side, the steam from heating water provides the input to the rule, the big piston outputs the steam into the vertical motion of the piston. That vertical motion, through the rod connecting the piston to the lever, is now a new input. The lever is a rule changing the direction of the motion connecting it to a wheel on the right side. This rule converts vertical motion to circular motion. The lights lines are belts to link the circular motion, yes a link is a rule to drive some other outputs, one of which is the governor. The governor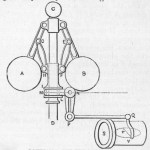 , that diamond shaped object with two balls attached in the middle of the diagram controls the speed of the engine spreading as it speeds off to reduce the steam output slowing the engine or narrowing to let more steam speed it up. Feedback enables a rule to modify the input based on the output.
, that diamond shaped object with two balls attached in the middle of the diagram controls the speed of the engine spreading as it speeds off to reduce the steam output slowing the engine or narrowing to let more steam speed it up. Feedback enables a rule to modify the input based on the output.
These are just a few of the functions that make up this function machine, converting heat to steam to drive a piston, to turn a wheel, to add more water, to… The function machines we build on spreadsheets work in the same ways, sometimes just multiplying a quantity, sometimes changing one form of data, or sometimes using the output to control the input. Though we may think about different things today than people did 300 years ago, we still build our ideas in much the same ways. We still build models as collections of functions.

I think it is important to make the point that a function, unlike for example, a program, can have one and only one output per input.