Math is not only the last letter in STEM or STEAM, it is the only one that we do not picture as experimental. We don’t imagine students learning science without doing experiments. We don’t imagine them learning technology without writing code, or learning engineering without building models, or learning art without messing with paint, clay, or paper. Yet, we easily imagine learning math without experimenting. In fact, it is rare that students ever do a math experiment or think about math that does not have a “right” answer.
I learned to experiment from one of my great teachers, Walt Hunter. I even had the great good fortune to also being his chemistry lab assistant my senior year in high school. That I did not fall in love with chemistry was not his fault; I had just loved physics since I was 7 years old. But I did fall in love with experimentation, and like Walt I gained a deep belief that learning to experiment should be an essential aspect of every student’s education. I brought that belief to my physics classes replacing teacher demonstration with student experimentation. I took it to my Jr. High math classes, where I made my students worksheets that let them play with numbers and mathematical patterns. I carried it to my focus on manipulatives as a math coordinator, and I bring it to What if Math.
Using spreadsheets as basic learning tools for math has many advantages, but I think the most important one is that it turns math into a laboratory science. It enables students to experiment, to build and iterate models, to test those models, and to apply them to real-world data, complex rich data. It lets them ask and answer what if… questions. And it turns them into explorers who love to use math and who gain Walt’s experimental habits of mind, the thrill of discovery. It is this, I now know, that Lynn Steen saw when he described mathematics as the “Science of Patterns,” for math does belong to STEM/STEAM after all. So, when you plan your math classes, imagine your chemistry teacher, and the twice weekly labs where you learned to act like a scientist, to explore, to discover, to ask, “What if…”
Art
*Portrait of Antoine-Laurent Lavoisier and his wife by Jacques-Louis David, ca. 1788, Wikipedia

 This image of James Watt’s early steam engine shows a variety of inputs, outputs, and connections between them. On the left side, the steam from heating water provides the input to the rule, the big piston outputs the steam into the vertical motion of the piston. That vertical motion, through the rod connecting the piston to the lever, is now a new input. The lever is a rule changing the direction of the motion connecting it to a wheel on the right side. This rule converts vertical motion to circular motion. The lights lines are belts to link the circular motion, yes a link is a rule to drive some other outputs, one of which is the governor. The governor
This image of James Watt’s early steam engine shows a variety of inputs, outputs, and connections between them. On the left side, the steam from heating water provides the input to the rule, the big piston outputs the steam into the vertical motion of the piston. That vertical motion, through the rod connecting the piston to the lever, is now a new input. The lever is a rule changing the direction of the motion connecting it to a wheel on the right side. This rule converts vertical motion to circular motion. The lights lines are belts to link the circular motion, yes a link is a rule to drive some other outputs, one of which is the governor. The governor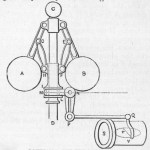 , that diamond shaped object with two balls attached in the middle of the diagram controls the speed of the engine spreading as it speeds off to reduce the steam output slowing the engine or narrowing to let more steam speed it up. Feedback enables a rule to modify the input based on the output.
, that diamond shaped object with two balls attached in the middle of the diagram controls the speed of the engine spreading as it speeds off to reduce the steam output slowing the engine or narrowing to let more steam speed it up. Feedback enables a rule to modify the input based on the output. Stand and deliver teaching puts the educational burden on the teacher. Students are the recipients of the knowledge in the head of the teacher. I am reminded of this old Egyptian image of Akhenaten’s god. In the paper classroom the teacher’s ability to motivate, to tell a story, to organize, and to simplify the textbook’s knowledge was nearly all of the content available to students. Stand and deliver was a reasonably efficient way to bring the content to the student. Eye contact, proximity, raised hand signals, and easy verbal interaction made this model sufficiently flexible, engaging, and rewarding.
Stand and deliver teaching puts the educational burden on the teacher. Students are the recipients of the knowledge in the head of the teacher. I am reminded of this old Egyptian image of Akhenaten’s god. In the paper classroom the teacher’s ability to motivate, to tell a story, to organize, and to simplify the textbook’s knowledge was nearly all of the content available to students. Stand and deliver was a reasonably efficient way to bring the content to the student. Eye contact, proximity, raised hand signals, and easy verbal interaction made this model sufficiently flexible, engaging, and rewarding.